Unbounded Non-Determinism

In the world of concurrent and distributed systems, not everything follows a predictable path. Some behaviors emerge not from fixed rules, but from timing, competition, and chance.

One such behavior is unbounded non-determinism — a subtle but powerful concept where systems may have infinitely many options to choose from, and no guarantee about when a choice will be made.

In this blog, we’ll break down what unbounded non-determinism really means, how it manifests in systems, and why it sits beyond the reach of traditional computation models like the Turing Machine.

Before we dive deeper into what makes unbounded non-determinism so special — and tricky — let’s first step back and understand non-determinism itself. What happens when a system is allowed to make choices — not based on inputs or logic, but arbitrarily?

What is Non-Determinism?

A non-deterministic system is one which can choose between multiple possible next steps from a given state, not necessarily based on input or past history. In simpler terms, it’s like making an arbitrary choice — but from a finite set of possibilities.

While non-determinism already introduces uncertainty by allowing multiple possible outcomes, it typically assumes those choices are finite — and made within a reasonable time.

But what happens when:

• The choices aren't just many, but infinite?
• And the time it takes to make a choice isn't just uncertain, but unbounded?

What is Unbounded Non-Determinism?

Unbounded non-determinism refers to a behavior in concurrency (multiple tasks running at once) where a process may face unpredictable delays or have infinitely many options to choose from at a given point. In other words, it can take infinite time to choose from infinite number of choices

This abstract definition may seem theoretical, but it has very concrete manifestations

Let’s consider a minimal yet powerful example — a message-passing system that demonstrates how timing alone can lead to unpredictable, unbounded outcomes.

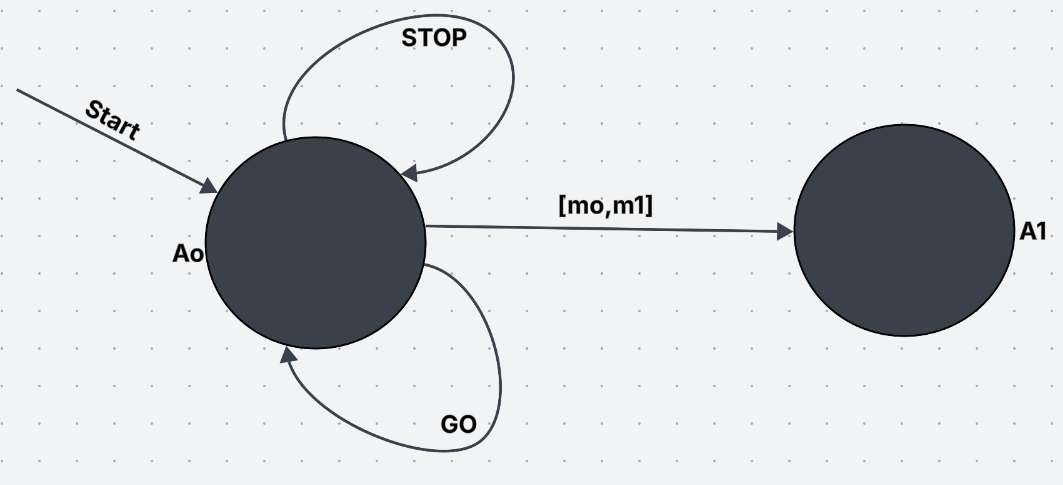
System Components:

• A₀ (the main active process):
  This is the core process responsible for handling messages and maintaining a counter.

  Messages involved:

  • start: Triggers the activation of A₀.
  • go: Instructs A₀ to increment a counter and send another "go" message to itself.
  • stop: Instructs A₀ to halt and report the final counter value.

• A₁ (final state):
  A passive state where the count is reported once A₀ halts — not involved during the counting loop.

• Initialization:
  A₀ is activated when it receives the "start" message.

• Parallel Message Sending:
  Upon starting, A₀ immediately sends two messages:

  • A go message to initiate the counting loop.
  • A stop message to eventually halt the process.

• Unbounded Looping (via go):
  Each time A₀ processes a go message:

  • It increments the counter by 1.
  • It sends itself another go message.

This creates a chain of self-recursive messages, with no predefined limit — allowing the process to increment indefinitely.

Termination (via stop):

• At some unpredictable point, the "stop" message arrives.
• A₀ halts upon receiving it, and reports the current counter value.
• The final count depends entirely on how many "go" messages were processed before the "stop" message is handled.

Why This Demonstrates Unbounded Non-determinism?

Once the process is started, there’s no limit to how many go messages might be processed before the stop message is finally handled. It could be zero, ten, a thousand — or just keep going indefinitely.

The system doesn’t enforce any upper bound, and it doesn’t make any conscious decision about when to stop. What makes this especially powerful — and unpredictable — is that nothing inside the system is choosing the outcome. There's no function saying, stop after N steps. Instead, the final count is shaped entirely by when the stop message happens to interrupt the ongoing go loop.

This is what makes the behavior truly non-deterministic and unbounded. The system reacts based on external timing and execution order, not internal logic. It’s like flipping a coin an unknown number of times — not because you're choosing to, but because the coin keeps getting tossed until someone yells stop, and you have no idea when that will happen.

As a result, the system's outcome isn’t just variable — it’s infinitely open-ended. And this lack of internal control or limits is exactly what places it beyond what a Turing Machine can simulate, making it a classic example of unbounded non-determinism in action.

Let's try bringing in the most powerful model of computation

The Turing machine

At its core, a Turing Machine works with a fixed set of states and rules. It knows exactly what to do at every step — read a symbol, update the tape, move left or right, transition to another state. Even if it’s non-deterministic, the choices it makes are still bounded and explicitly defined in the machine's transition function.

What it can’t do is make a decision based on something like, stop whenever a random message happens to arrive. It can’t say, just keep going until an unknown external event interrupts me. If you want a Turing Machine to halt after N steps, you have to encode that number N into the machine itself — there’s no room for arbitrary timing or external influences.

But in the stop and go system we’ve described, the outcome — the final count — is determined not by logic, but by timing. It halts when the stop message happens to get processed, which could be after any number of steps. There’s no rule deciding that — and crucially, the process running inside the system doesn’t know or control when that will happen.

A Turing Machine simply isn’t built to handle this kind of behavior.

Let’s take this a step further. Even if we bring in a formal model — like Dijkstra’s model of distributed systems

Dijkstra’s model

In Dijkstra’s model, the system is designed with a bounded number of global states — that is, due to finite code and memory, the total number of unique configurations the system can be in is limited.

However, Dijkstra allows for unbounded delays in servicing requests. This means a task (like a message or a process waiting to be executed) can be postponed indefinitely, even though the system keeps running.

Now here’s where the contradiction appears:

• Since the number of possible states is finite, and the system is allowed to delay endlessly, it will eventually revisit the same state — this is a direct consequence of the Pigeonhole Principle.

• But if a request is still waiting to be serviced during this repetition, the system can loop forever through these same states, never making any actual progress.

• It’s not that the system halts — it’s worse: it continues to run, but the waiting request is stuck in limbo, never reaching completion.

This creates a scenario where a system appears active but is actually failing to make forward progress — a classic case of livelock or starvation.

In the context of our go/stop system: The stop message may never be serviced if the system keeps cycling through go messages. The counter increases, the process seems alive, but the outcome — halting and reporting the count — never arrives. The system’s freedom to delay becomes its biggest flaw.

Solution?

Fairness

Since a process can be delayed indefinitely or be forced to wait while the system explores infinitely many choices, there’s no guarantee that every process will eventually get a chance to proceed. This can lead to starvation, where a task that’s always ready never gets executed.

Fairness, in this context, refers to the guarantee that every enabled process will eventually make progress, no matter how many other options or delays exist. It ensures that the system does not ignore certain tasks forever — even if it has an infinite number of decisions to make.

This idea of fairness isn’t like flipping a fair coin forever. With a coin, random chance means you’d eventually see both heads and tails, but there’s no rule forcing it—pure luck could delay one outcome for an arbitrarily long time. In unbounded nondeterminism, fairness isn’t about hoping every step happens; it’s a strict requirement that they do, regardless of chance.